AMICALE DES ANCIENS DE L'ECOLE NORMALE WILLIAM PONTY

Je souhaiterais, sans prétention académique aucune, vous entretenir d'un savoir-faire important : l'exploitation d'une courbe. 

Ce savoir-faire est utile, très  utile dans divers domaines, aussi bien en Sciences Physiques, qu'en Sciences de la Vie et de la Terre, Histoire et  Géographie ou Sciences Economiques.
L'exploitation d'une courbe fait partie des questions souvent posées en Sciences Physiques au Baccalauréat. Cette question particulière est la bête  noire de la plupart des candidats.

Pourtant cette notion est introduite, très tôt, en Sciences Physiques, d'abord en 4ème avec la courbe du poids (P) en fonction de la masse (M) et ensuite en 3ème  avec le tracé de la tension (U) en fonction de l'intensité du courant (I).

Mais malgré cela, cette notion pose encore problème, tout au long du Secondaire. En témoignent amplement les faibles performances des élèves, chaque fois cette compétence est demandée dans les évaluations.

Pourquoi cette notion est-elle si mal maîtrisée ?

A mon avis, la faute en incombe, à  la fois, aux Physiciens et aux Mathématiciens qui sont allés vite en besogne dans l'installation de ce savoir-faire. En n'abordant que des exercices très simples, mes collègues  ont traité trop superficiellement cette question, rendant la tâche très difficile aux apprenants  évalués  le plus souvent, sur des cas plus compliqués. 

Comment pourrait-on remédier à  cette situation ?

Encore à mon humble avis, il convient de réinstaller, pas à  pas, ce savoir complexe, indispensable aux Scientifiques. 

J’estime que, en 3 exercices, on peut enseigner cette notion de façon sûre et durable. 

Dans ces 3 exercices, l'élève aura à  répondre  à  la même  question : Quelles sont les coordonnées  de M1, un point d'une courbe déjà tracée?

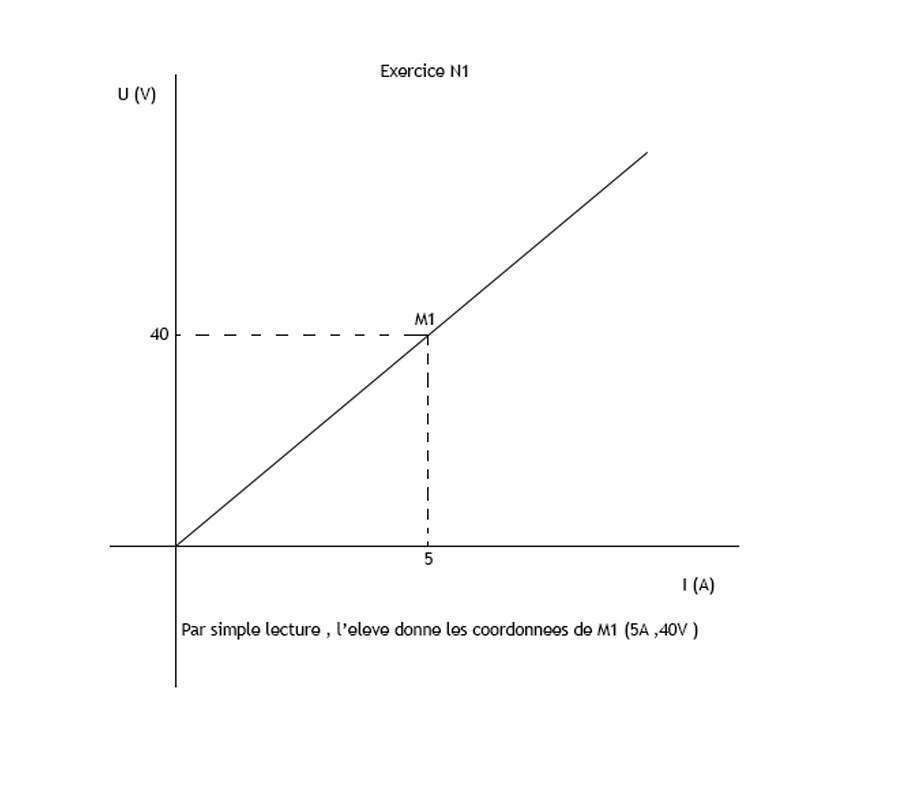
Dans le premier exercice, les coordonnées de M1 sont sur le schéma. L'élève répondra par une simple lecture. 

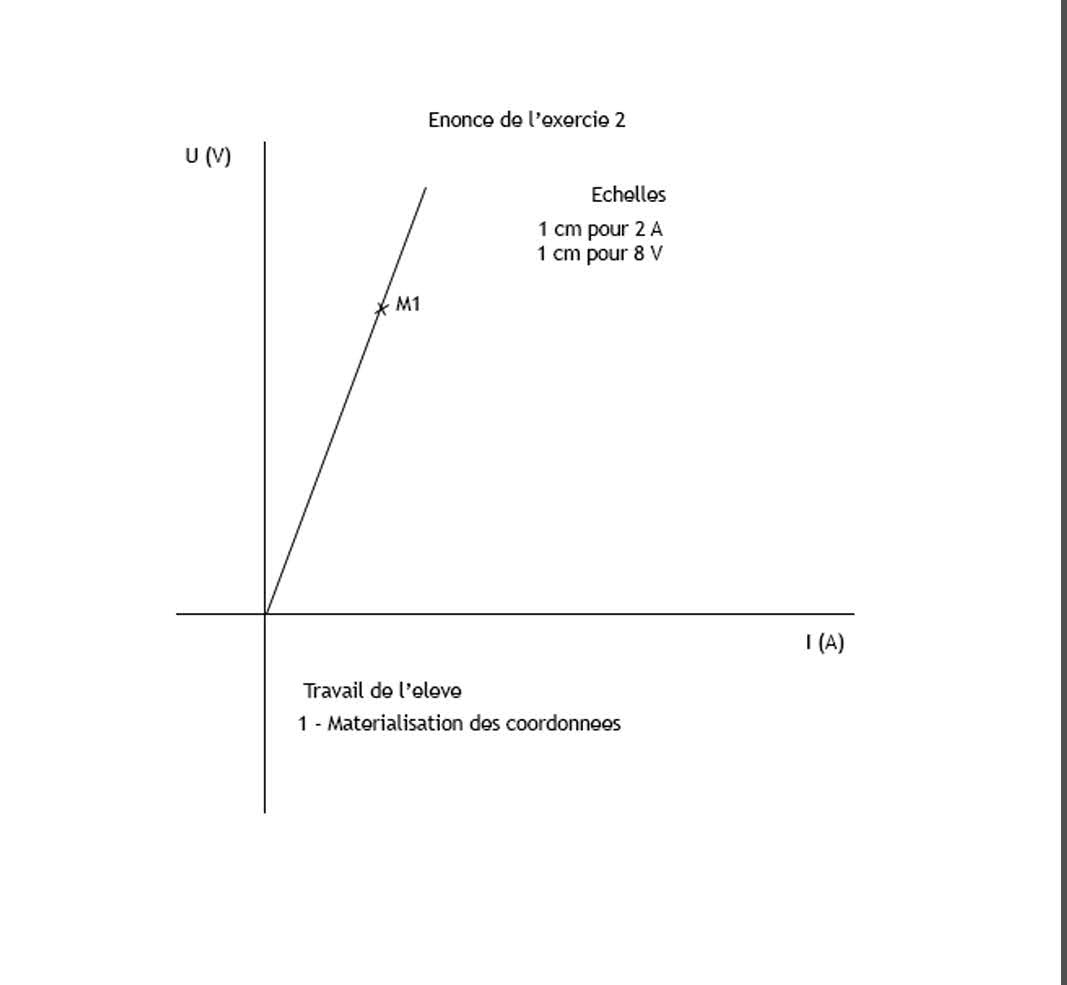
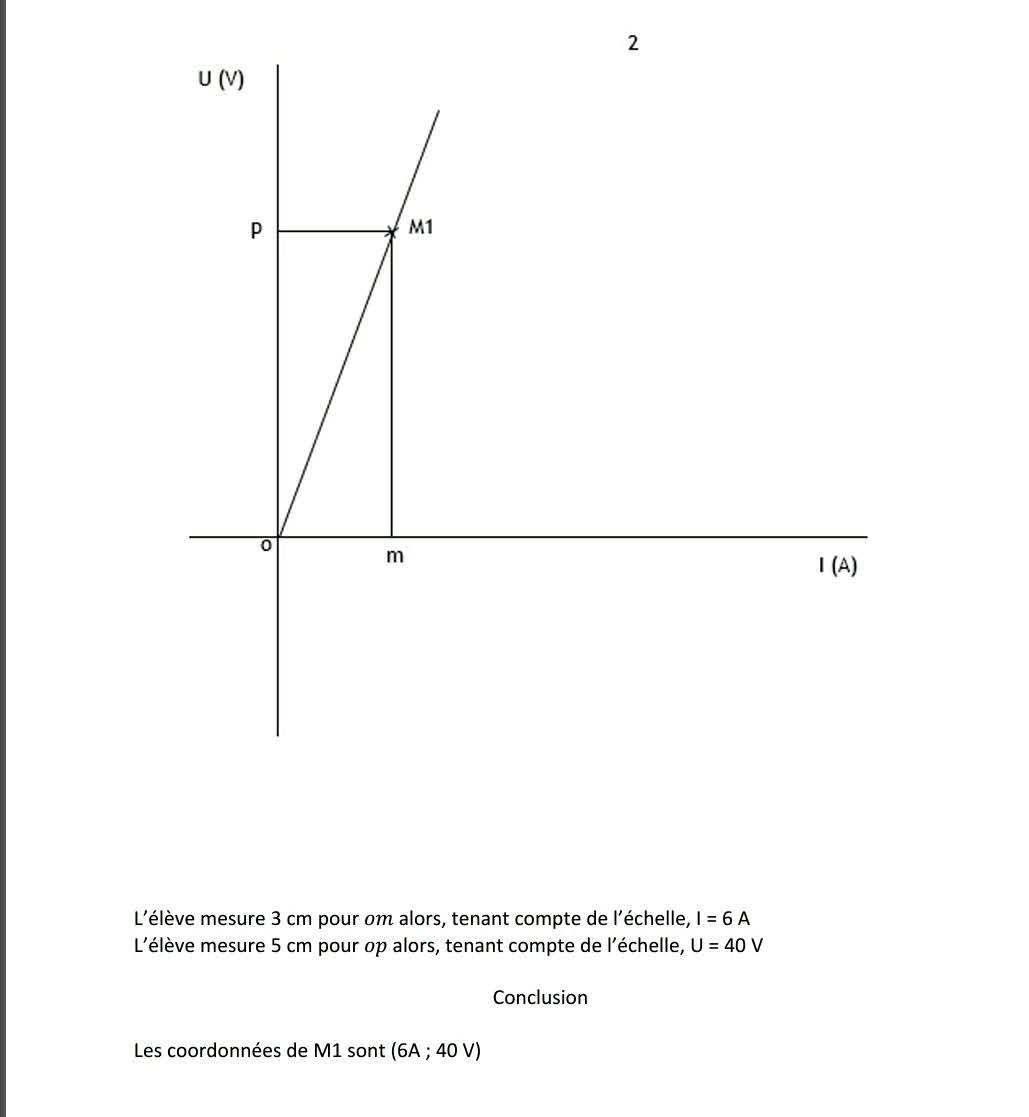
Dans le second exercice, l'échelle  sur les deux axes est donnée. L'élève devra, d'abord matérialiser les coordonnées de M1, ensuite mesurer une longueur, et  enfin tenir compte de l'échelle, avant de donner la réponse. 

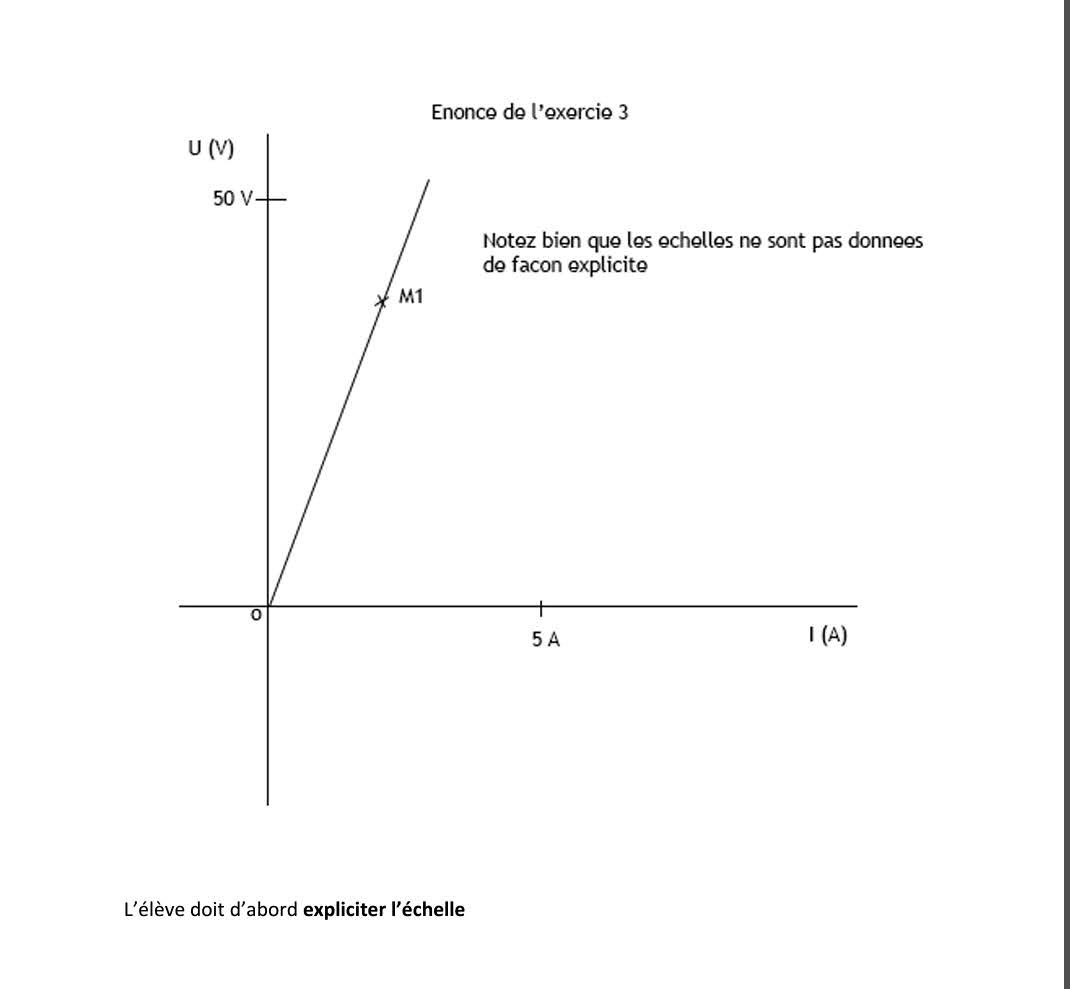
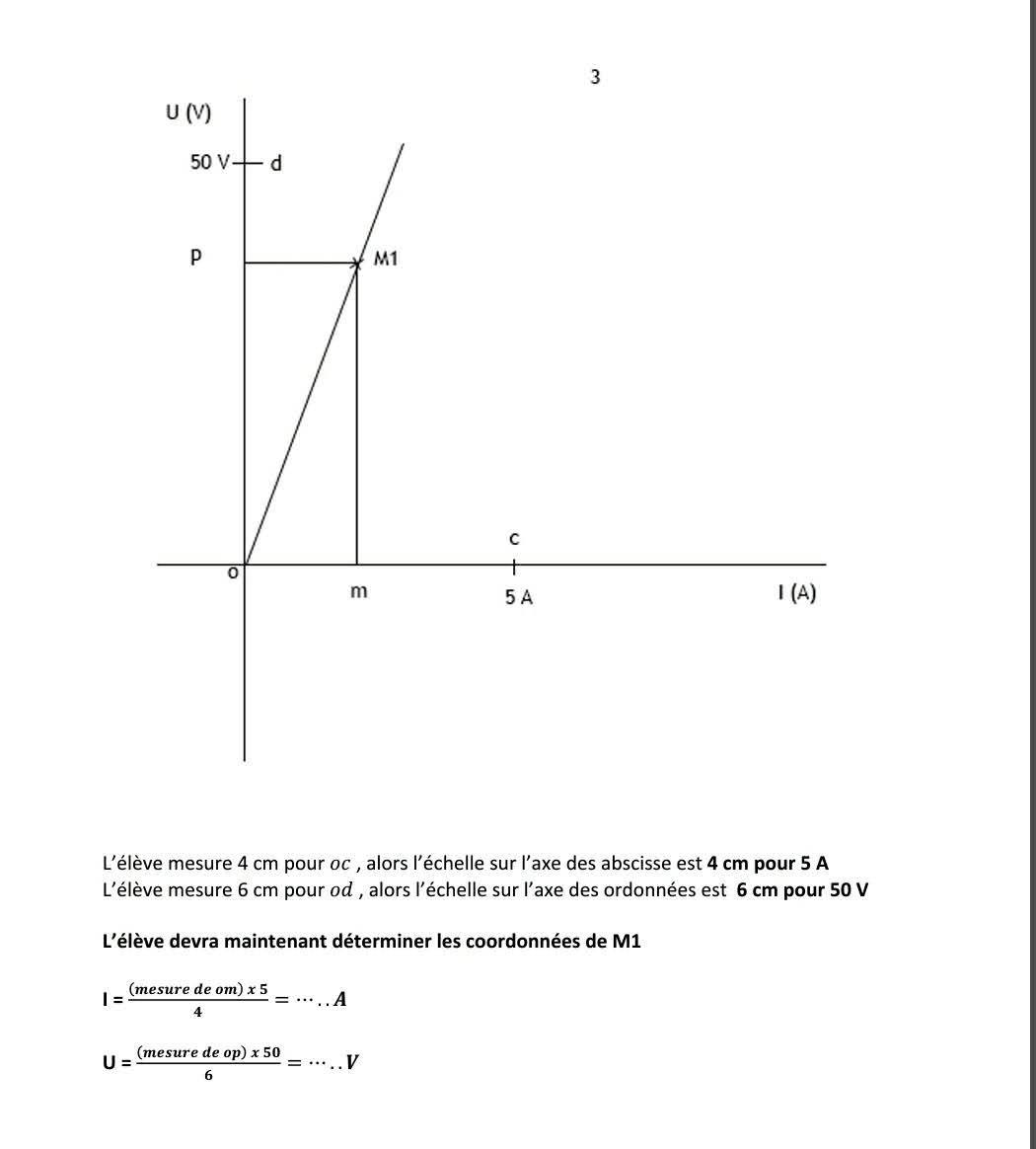
Passons au troisième problème. L'échelle n'est pas donnée, mais quelques valeurs sont indiquées sur chaque axe. 

Dans cet exercice, l'échelle  est implicite ; l'apprenant devra  l'expliciter.
En mesurant les longueurs qui correspondent aux valeurs sur les axes, l'élève déterminera l'échelle sur chaque axe. 

Ainsi, on ramène la résolution de l'exercice 3 à  celle de l'exercice 2.

Et on constate facilement que les 3 exercices ont été classés par difficulté croissante. 

Je demande sincèrement pardon à  ceux qui pourraient trouver ce développement trop technique.

 
Mais quels enseignements tirer de tout cela ?

Que les notions fondamentales devraient être abordées, étape, par étape, allant du plus facile au plus difficile, en insistant, dans le cas qui nous concerne aujourd'hui,  sur le respect de l’échelle.

Si nos élèves  ont des difficultés dans la maîtrise de certains savoir-faire en Sciences Physiques, les Enseignants en sont, en partie, les principaux responsables, car ils oublient qu’ils sont des Experts, alors que les apprenants  sont des novices. 

Si je peux donner un conseil aux Enseignants, c’est celui-ci : Chers collègues, procédez toujours par étape  pour installer les notions essentielles. 

  (*) Enseignant en Sciences Physiques